広告のレスポンスやLPのコンバージョン率を上げるために行われる、A/Bテスト。実は統計的に正しくないテスト結果にもとづいて、売上アップに貢献しない「改善」が行われがちであることをご存知ですか?マーケティングの現場で起こりがちなケースをもとに、「誤差」や「有意差」などについて、統計学の知識がない方にも分かりやすく解説します。
通販事業の現場で使われているKPIを新任担当者でも分かるようにまとめました。
⇒解説資料はこちら
目次
A/Bテストの結果、本当に正しい!?EC企業で起こった“事件”
広告のCPA改善やランディングページ(LP)のコンバージョン率(CVR)アップのために欠かせない、A/Bテスト。
このA/Bテストで数字が良かったクリエイティブを採用したら、費用対効果が悪化してしまった・・
そんな現象が起こってしまう可能性があることを、ご存知ですか?
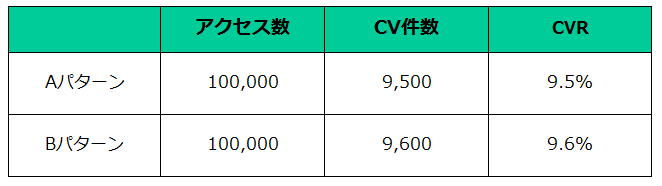
あるECサイトを運営する企業では、A/Bテストを継続的に実施してWEBサイトの CVRを改善してきました。
直近のデザイン改善でも「CVRが、9.5%から9.6%にアップ!」という結果が出て、社内の関係部署は祝福ムードに包まれていました。
(出典:「統計学が最強の学問である」西内啓)
このテスト結果について相談を受けた統計学者(著者)が、「誤差でもこれくらいの差が生じるのか?」「それとも、本当に改善したと言えるのか?」を確かめることに。
「カイ二乗検定」という手法で解析してみたところ、「実際には何の差もない状況でも、データの誤差によってこの程度の差が生じる確率は、44.7%である」という結果が示されました。
これは簡単に言うと「約半分の確率で、以前と変化しない」ということ。
つまり、A/Bテストによって「コンバージョンが改善した!」と判断されて採用されたデザインが、「売上アップに貢献するか?」はまったく未知数という衝撃的な結果が示されたのです。
通販事業の現場で使われているKPIを新任担当者でも分かるようにまとめました。
⇒解説資料はこちら
レスポンスが“逆転”してしまった・・化粧品チラシでの体験
このようにA/Bテストで「改善した!」と出た結果が、実は信頼できない数字だったという体験は、弊社でも実際にありました。
(参考:「そのA/Bテストの結果、信頼できる?統計が苦手な人向け、有意差の検定法」)
化粧品のチラシでキャッチコピーを変えて、2パターンのチラシを作成したのですが、1回目はAパターンの勝利。
ですがレスポンスの差が110%と大きくはつかなかったため、念のため別の媒体でも同じく2パターンを出稿したところ、2つ目の媒体では「Bパターンが、数件の差で多い」と結果が逆転。
さらに3つ目の媒体では、10件近くの差がついて、BパターンのレスポンスがAパターンを上回りました。
このように、3つの媒体でそれぞれバラバラの結果が出てしまったのです。
なぜ、このようにA/Bテストで全く異なる数字が測定されてしまうのでしょうか?
それは、「誤差」によって、実際のテスト結果は変動してしまうからです。
通販事業の現場で使われているKPIを新任担当者でも分かるようにまとめました。
⇒解説資料はこちら
テスト結果を狂わせる、「誤差」の正体とは?
誤差とは「実際に得られた値が、本来の値からどれだけずれているかを表す量」のこと。
データを測定したサンプル数が少ないと、偶然によって結果がブレて逆転してしまうことがあります。
「1人の顧客が反応したか?しなかったか?」「たまたま途中で心変わりした」といった些細なできごとが、テスト結果に影響を与えてしまうのです。
サンプルの少なさゆえのデータのバラツキによって、多くの回数で行った時の平均値、つまり広告やLPの持つ“本来の力”からテスト結果がずれてしまうこと。
A/Bテストにおける「誤差」の正体です。
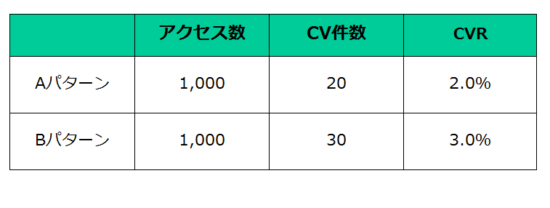
たとえば、LPのA/Bテストで、次のような結果が出たとしましょう。
Aパターンはコンバージョン率(CVR)が2%、Bパターンは3%。
この結果にもとづいて、「Aパターンの方が売れる」と結論づけられるのでしょうか?
テスト1
答えはNo.です。
Aパターンのコンバージョン(CV)が20件という数値は、誤差の観点を入れて考えると、ブレがあるなかで偶然に出てきた数値です。
同じくBパターンもブレがあるなかで出てきた数値ですが、お互いにブレのなかでも「はっきりとした差がある」言えるほどの数字ではないのです。
通販事業の現場で使われているKPIを新任担当者でも分かるようにまとめました。
⇒解説資料はこちら
ユーザーの購買行動が、「正規分布」にしたがうなら
続いて、次の数字ならどうでしょうか?
AパターンはCVRが2%、Bパターンは3%とここまでは先ほどの数字と同じです。
ただし、アクセス数が10倍に増えて、10,000に。
CV件数もそれぞれ、200件と300件になっています。
テスト1
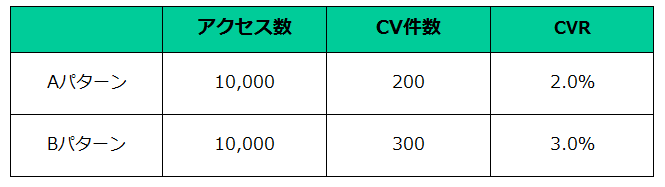
結論から言うと、このテスト結果は十分に信頼できると判断できます。
なぜ、このように判断できるのでしょう?
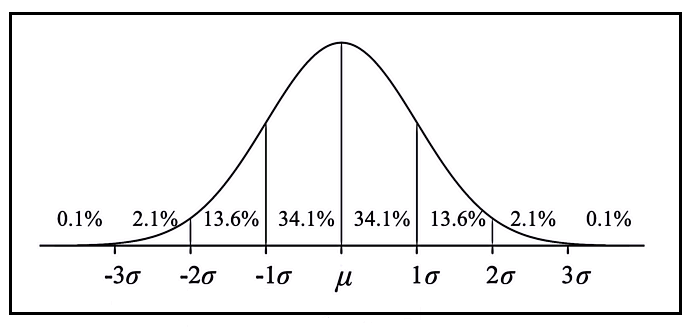
WEBサイトのコンバージョン、つまりユーザーが「買うか?」「買わないか?」といった現象は、一般的に「正規分布」にもとづくと考えられています。
正規分布とは、下図のように「左右対称で滑らかな曲線の山で表されるデータのバラつき方」のことです。
(出典:「統計学が最強の学問である[実践編]—データ分析のための思想と方法 」西内啓)
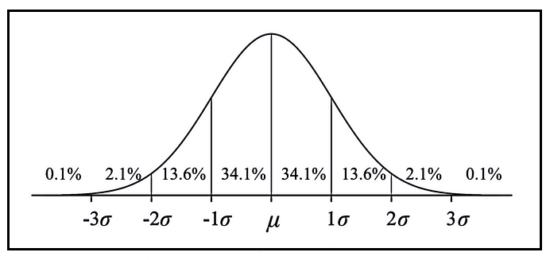
「コインを投げたときに表が出る回数」や「日本人の身長」、あるいは「センター試験の成績」といった数多くの現象について、数字の散らばり方が正規分布にしたがうことが分かっています。
通販事業の現場で使われているKPIを新任担当者でも分かるようにまとめました。
⇒解説資料はこちら
アクセス数を増やしたら、AとBパターンの差は「有意差」に
この正規分布にしたがう場合、限られたアクセス数のもとに出た「CVR2%」や「3%」という平均値から、「本来の正しいCVR、すなわちアクセス数が無限に近いほど多かったときに出るCVRがどの範囲にあるか?」を推定できます。
テスト1では、AパターンとBパターンで本来のCVRが取りうる範囲(「信頼区間」と呼びます)が重なってしまいます。
したがって、テスト結果は統計的には誤差の範囲と推定されます。
テスト1

逆にテスト2では、AパターンとBパターンは信頼区間が重なりません。
したがって、テスト結果は統計的に十分に正しいと推測されます。
テスト2
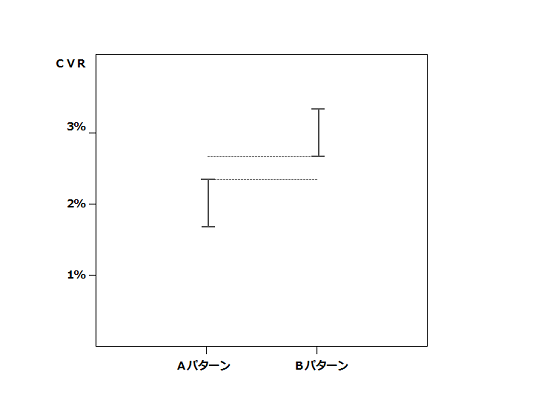
このことを統計的に「有意」である、「有意差」が付いていると言います。
(参考:「A/Bテストの結果をどのように解釈するか?」)
このように比較的に多いアクセス数のもと、AパターンとBパターンの結果に十分な差がついていると、統計学の観点からも「誤差の範囲」ではなく、「信頼できる結果」と言える可能性が高くなるのです。
では、このようにAパターンとBパターンが有意差がついているか?は具体的にどうやって求めればよいでしょうか?
「仮説検定」などを活用して有意差を判定する方法については、統計学を学んだことのない“文系”の方にも分かりやすいように、また記事を書く予定です。
通販事業の現場で使われているKPIを新任担当者でも分かるようにまとめました。
⇒解説資料はこちら

